문제
https://www.acmicpc.net/problem/1629
자연수 A를 B번 곱한 값을 C로 나눈 나머지 구하기
A, B, C는 모두 2,147,483,647 이하의 자연수
풀이
A, B, C가 매우 큰 값이므로 직접 A^B%C를 구할 수 없다. (오버플로우 발생)
A^B라는 매우 큰 값을 작은 값으로 분할하여 나머지 연산을 해야 한다.
- 분할 : A^B를 작은 값들의 곱으로 치환(아래 그림처럼 B가 짝수일 때, 홀수일 때 다르게 치환됨)-> A^1 될 때까지 분할하기

2. 합병 : 작은 값들을 연산한 후 합쳐서 큰 값의 해를 구하기를 반복한다.
여기서 중요한 작업 : 작은 값들을 합쳐 큰 값의 해를 구할 때 [모듈러 연산의 분배 법칙]을 적용해준다.
- 모듈러 연산의 분배 법칙
(a + b) % m = ((a % m) + (b % m)) % m
(a * b) % m = ((a % m) * (b % m)) % m
(a - b) % m = ((a % m) - (b % m) + p) % m # 음수 방지
(증명은 다음과 같다.)
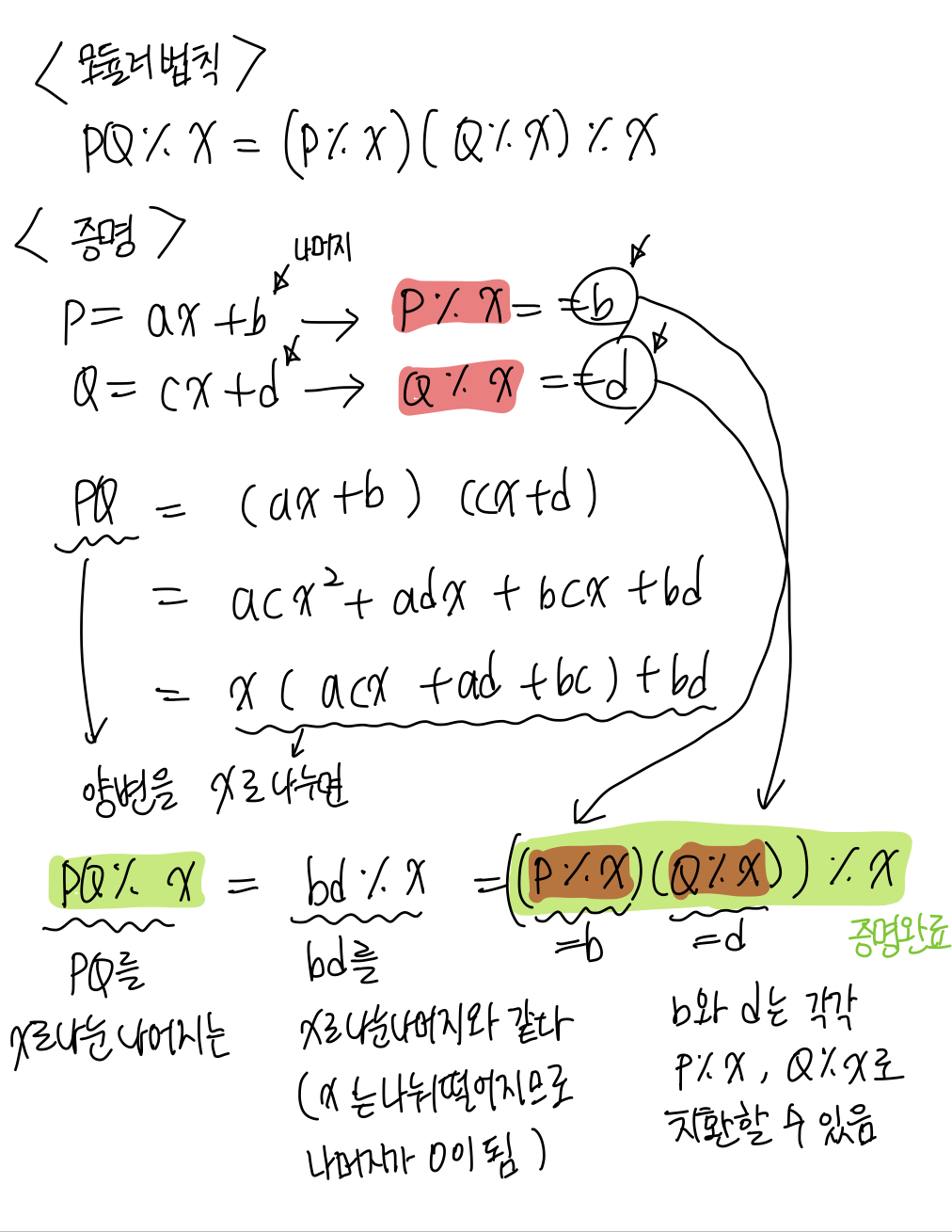
P=ax+b, Q=cx+d 로 가정하면
P*Q = x(acx+ad+bc)+bd 형태가 된다.
여기서 양변을 x로 나누면
P*Q를 x로 나눈 나머지 (P*Q%x)는 bd를 x로 나눈 나머지(bd%x)와 같아지게 된다.
x(acx+ad+bc)부분은 x로 나누면 나머지가 0이기 때문에 신경쓰지 않아도 된다.
앞서 P=ax+b는 P를 x로 나눈 나머지가 b, Q=cx+d는 Q를 x로 나눈 나머지가 d라는 의미이므로
각각 P%x를 b로, Q%x를 d로 치환할 수 있다.
이로써 PQ%x = ((P%x)(Q%x))%x가 증명되었다.
출처:
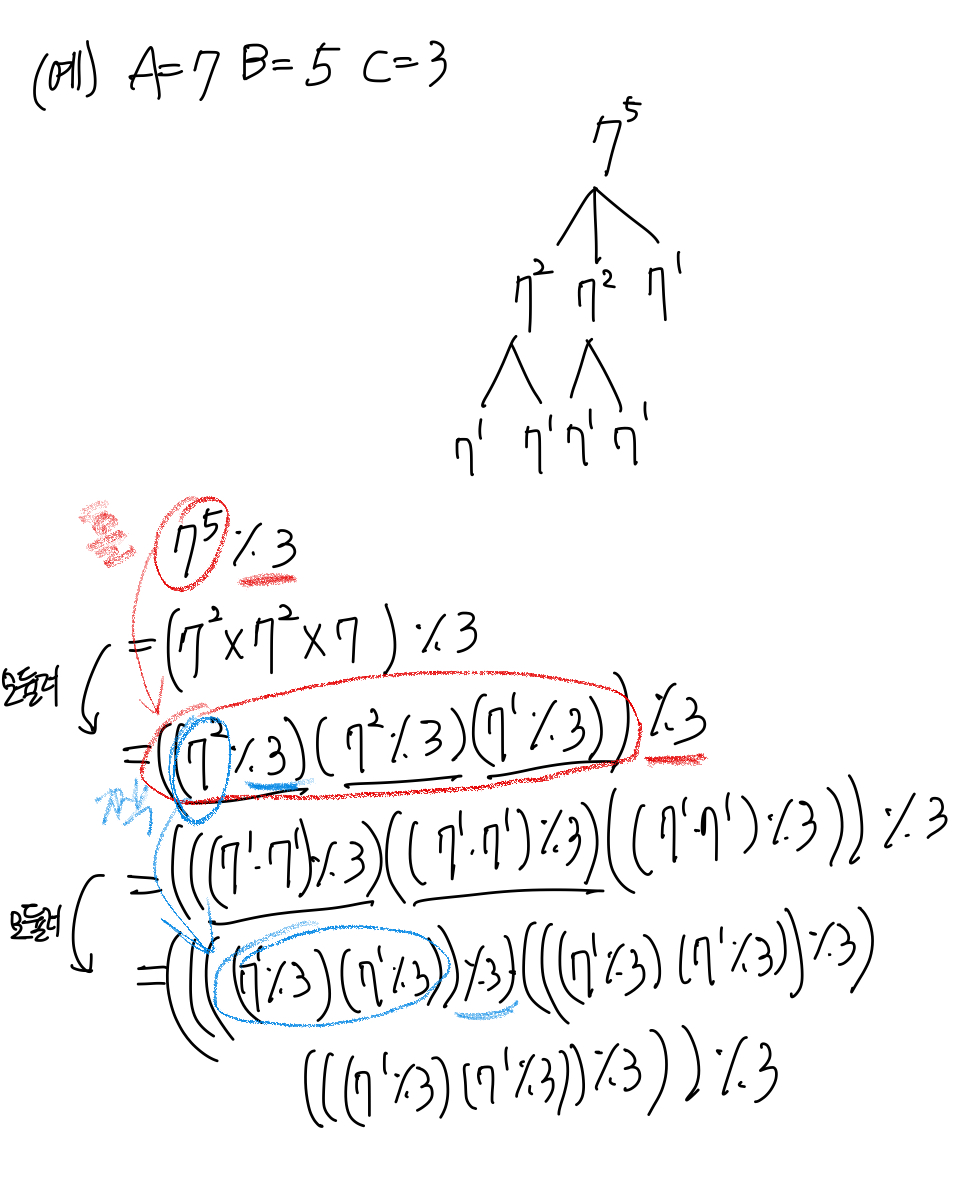
모듈러 분배 법칙을 이용하여 (7^5)%3을 작은 연산들로 치환해보자.
제곱수가 1이 될 때까지 분할하면 다음과 같은 사실을 알 수 있다.
- 재귀로 리턴받은 값 마다 나머지 연산(%C)을 해야 한다.
- B가 짝수이면 A^(B//2)%C를 두 번 재귀호출하고 두 값을 곱한 후 나머지 연산(%C)
- B가 홀수이면 A^(B//2)%C를 두 번, A^1을 한 번 재귀호출하고 세 값을 곱한 후 나머지 연산(%C)
- base condition(모든 입력 값에 대해 귀결되는 조건)은 A^1 값이다. 이 값도 %C로 나머지 연산을 해줘야 한다.
틀린 부분이나 궁금한 점이 있다면 댓글 달아주세여
코드
import sys
A, B, C = map(int, sys.stdin.readline().split())
def solve(a, b, c):
if b==1: # base condition: 가장 작은 값으로 분할했다면 나머지 계산해서 리턴해주기
return a%c
tmp = (solve(a, b//2, c) % c)
if b%2==0: # 짝수일 때
return (tmp * tmp) % c
else: # 홀수일 때
return (tmp * tmp * (a%c)) %c
print(solve(A, B, C))
References
https://alive-wong.tistory.com/59
모듈러 분배 법칙의 이해 - 나머지 연산 분배 법칙
사칙 연산과 마찬가지로, 정수의 나머지에 대해서도 연산 개념이 존재한다. 코딩 테스트에서 명시적으로 나머지 연산의 결과를 요구할 때가 있다. 또는 풀이 과정에서 나머지 연산 중 수가 너무
alive-wong.tistory.com
https://w00ye0l.tistory.com/67
[백준/Python] 1629번: 곱셈
https://www.acmicpc.net/problem/1629 1629번: 곱셈 첫째 줄에 A, B, C가 빈 칸을 사이에 두고 순서대로 주어진다. A, B, C는 모두 2,147,483,647 이하의 자연수이다. www.acmicpc.net 문제 분석 문제는 A를 B번 곱한 수를
w00ye0l.tistory.com
참고
- 나머지 연산 '분배'법칙이 왜 필요할까?
모듈러 연산(=나머지 연산)은 다른 사칙연산에 비해 처리 비용이 높기 때문에 매우 큰 값을 모듈러 연산하면 오버플로우가 발생한다.
참고로 a, b를 모듈러 연산하면 a%b = a-b * (a/b)인데, 절차는 다음과 같다.
1. a/b로 몫을 구하고
2. b*a/b을 구하고
3. a-(b*a/b)를 수행하여 나머지를 구한다.
나눗셈 연산 자체도 cpu에서 처리 비용이 높은데, 내부적으로 연산 횟수도 많고 나눗셈도 포함하고 있어서 부하가 크다.
따라서 매우 큰 값에 모듈러 연산을 수행하면 안 되고 연산 과정 도중에 모듈러 연산을 적용해야 한다.
-> 모듈러 연산의 분배 법칙을 알아야 함
'정글 > 알고리즘' 카테고리의 다른 글
| [백준/Python] 2470번 : 두 용액 (0) | 2025.03.23 |
|---|---|
| [백준/Python] 10830번 : 행렬 제곱 (0) | 2025.03.23 |
| [백준/Python] 2805번 : 나무 자르기 (0) | 2025.03.21 |
| [백준/Python] 9095번 : 1, 2, 3 더하기 (0) | 2025.03.20 |
| [백준/Python] 1914 : 하노이 탑 (0) | 2025.03.20 |